Алгоритм Дейкстры
Создана 25.06.2024
Отредактирована 25.06.2024
Отредактирована 25.06.2024
В видео рассматривается алгоритм нахождения кратчайшего пути, созданный нидерландским учёным Эдсгером Дейкстрой в 1959 году. Алгоритм Дейкстры позволяет найти кратчайшие пути от одной из вершин графа, называемой источником, до всех других вершин графа. Алгоритм может быть использован только на графах с неотрицательными весами дуг.
Автор данного видео Царев Роман Юрьевич, преподаватель Сибирского федерального университета, представляет на своем канале видео, связанные с информационными технологиями.
Я лишь дам некоторое объяснение к алгоритму с точки зрения откуда и как берутся значения, так как мне был немного не понятен этот аспект, это моя особенность с института. Возможно, вы с первого раза все поняли, а если нет, то это вам поможет.

Для нахождения искоммых значений, применяется формула ниже:
D[v]: = min(D[v], D[w] + C[w, v])
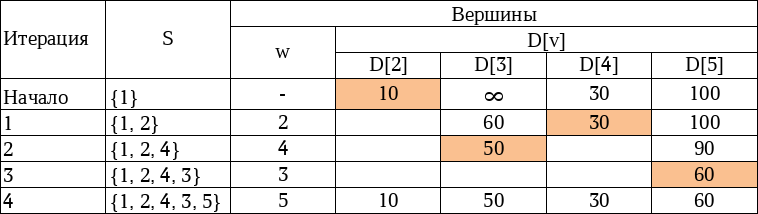
Начало
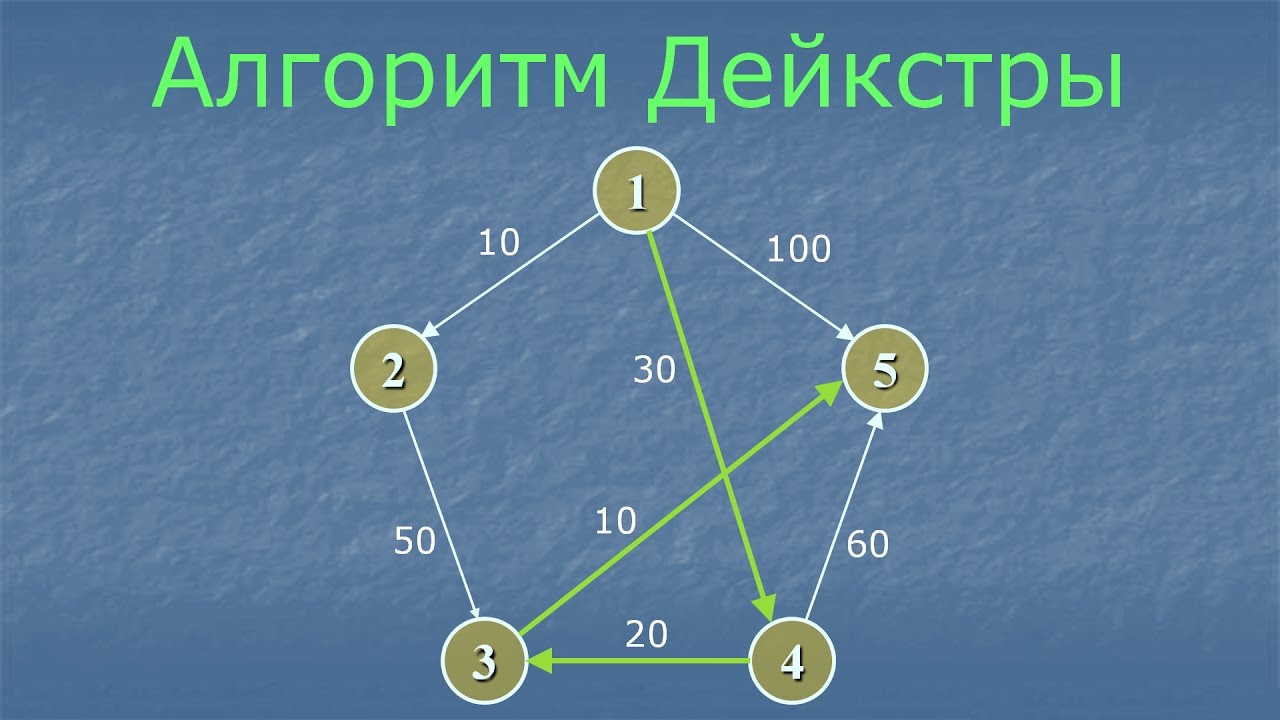
Значения 10, ∞, 30, 100 это стоимость дуг от вершины 1 до вершин 2, 3, 4, 5.
Обратите внимание на знак ∞, так как прямой дуги не существует между вершинами 1 ---> 3, то мы обозначаем стоимость этим знаком.
Пройдемся по всем остальным строкам с 1 по 4 этерациям.
Итерация 1
Рассмотрим как были вычислены значения для вершин D[3] = 60, D[4] = 30, D[5] = 100, по формуле выше:
D[3]: = min(D[3], D[2] + C[2, 3]), где
D[v] = D[3] - это предыдущее значение, значения D[3] = ∞
D[w] = D[2] - это наименьшее значение, равное 10 на предыдущем шаге (начало)
C[w, v] = C[2, 3] - стоимость дуги от вершины 2 к вершине 3 равное 50
выбираем минимальное значение между ∞ и 60 (10 + 50), где D[3]: = 60
D[4]: = min(D[4], D[2] + C[2, 4]), где
D[v] = D[4] - это предыдущее значение, значения D[4] = 30
D[w] = D[2] - это наименьшее значение, равное 10 на предыдущем шаге (начало)
C[w, v] = C[2, 4] - стоимость дуги от вершины 2 к вершине 4 равное ∞, так как такой вершины не существует
выбираем минимальное значение между 30 и ∞ (10 + ∞ = ∞), где D[4]: = 30
D[5]: = min(D[5], D[2] + C[2, 5]), где
D[v] = D[5] - это предыдущее значение, значения D[5] = 100
D[w] = D[2] - это наименьшее значение, равное 10 на предыдущем шаге (начало)
C[w, v] = C[2, 5] - стоимость дуги от вершины 2 к вершине 5 равное ∞, так как такой вершины не существует
выбираем минимальное значение между 100 и ∞ (10 + ∞ = ∞), где D[5]: = 100
Итерация 2
Рассмотрим как были вычислены значения для вершин D[3] = 50, D[5] = 90, на второй итерации:
D[3]: = min(D[3], D[2] + C[4, 3]), где
D[v] = D[3] - это предыдущее значение, значения D[3] = 60
D[w] = D[4] - это наименьшее значение, равное 30 на предыдущем шаге (Итерация 1)
C[w, v] = C[4, 3] - стоимость дуги от вершины 4 к вершине 3 равное 20
выбираем минимальное значение между 60 и 50 (30 + 20 = 50), где D[3]: = 50
D[5]: = min(D[5], D[2] + C[4, 5]), где
D[v] = D[5] - это предыдущее значение, значения D[5] = 100
D[w] = D[4] - это наименьшее значение, равное 30 на предыдущем шаге (Итерация 1)
C[w, v] = C[4, 5] - стоимость дуги от вершины 4 к вершине 5 равное 60
выбираем минимальное значение между 100 и 90 (30 + 60 = 90), где D[5]: = 90
Итерация 3
Рассмотрим как было вычислено значение для оставшейся вершины D[5] = 60, на третьей итерации:
D[5]: = min(D[5], D[2] + C[3, 5]), где
D[v] = D[5] - это предыдущее значение, значения D[5] = 90
D[w] = D[3] - это наименьшее значение, равное 50 на предыдущем шаге (Итерация 2)
C[w, v] = C[3, 5] - стоимость дуги от вершины 3 к вершине 5 равное 10
выбираем минимальное значение между 90 и 60 (50 + 10 = 60), где D[5]: = 60